Anova

Lecture ?

Dr. Elijah Meyer

NC State University
ST 511 - Fall 2024

2024-10-16

Checklist

– Take-home exam due Friday (11:59pm)

– Keep up with exam-1 Slack

– No quiz this week

– No hw this week

Announcements

– I’ll have the in-class graded by Friday afternoon (Sunday by the latest)

– I’ll make an announcement on exam corrections once I see the grade distribution

  > Won't be the entire exam (1 or 2 questions)

Wrap up unit 1: review

Suppose you calculate a p-value of -0.147. From this, you can determine that…

– You have an observed statistic that is really unlikely to be observed under the assumption of the null hypothesis

– You made some arithmetic mistake. P-values can not be negative

– Your test statistic is negative

– Every value in your data set is negative

Wrap up unit 1: review

Suppose a researcher, using a t-distribution with 20 degrees of freedom, calculated a p-value to be 0.076. Assuming that everything else regarding the study stayed exactly the same, what would happen to the p-value if we used a t-distribution with 5 degrees of freedom…

– The p-value would be larger

– The p-value would be smaller

– The p-value would stay exactly the same

Wrap up unit 1: review

Assuming the Central Limit Theorem assumptions are met, what would you expect the shape of the population distribution be of all Iris flower’s petal length?

– Normally distributed

– Left skewed

– Right skewed

– Not enough information to answer the question

Wrap up unit 1: review

Regardless of your answer part g, assume you calculated the following 90% confidence interval for the population mean petal length (0.758, 6.758). Interpret this confidence interval in the context of the problem.

New Content

Inference on many means

We will use the penguins data set for the slides example, and practice with a new data set for an AE example (Monday).

Inference on many means

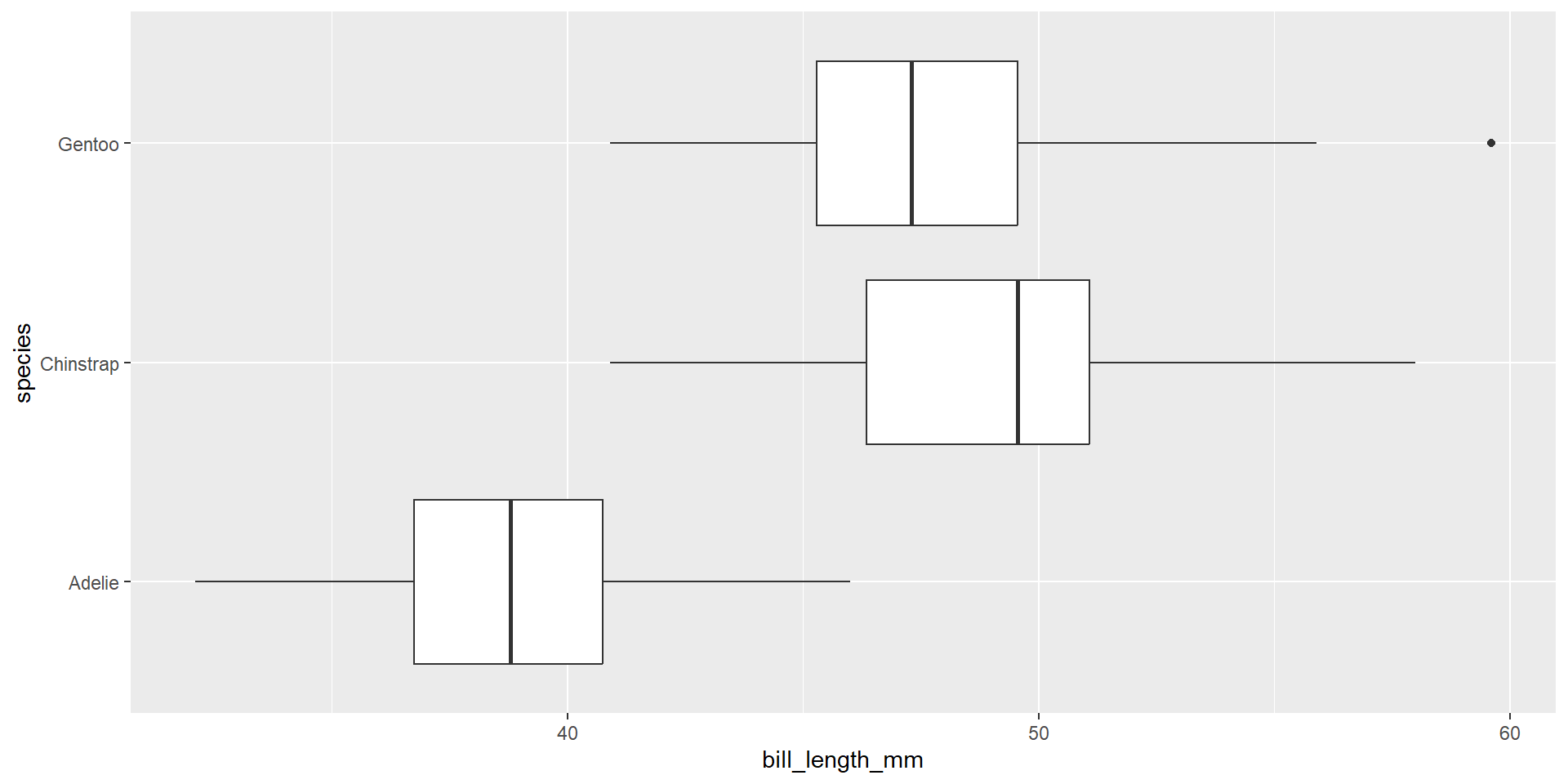
In our last example, species impact on bill length. We limited our question to Gentoo and Chinstrap penguins. How species or penguin are in the data set?

Anova

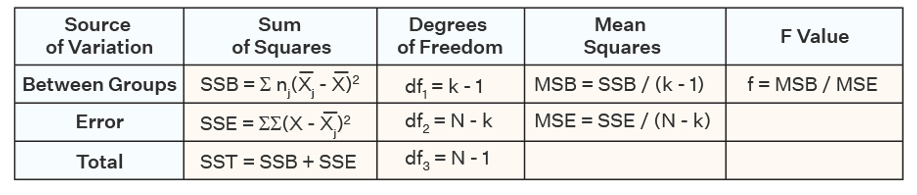
Analysis of variance (ANOVA) is used to test whether the mean outcome differs across two or more groups.

ANOVA uses a test statistic, the F-statistic, which represents a standardized ratio of variability in the sample means relative to the variability within the groups.

The Big Idea

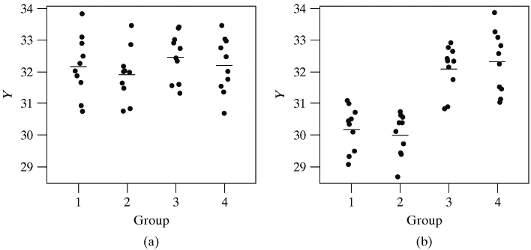
The Big Idea

Theory based

If we assume \(H_o\) is true and the model conditions are satisfied, an F-statistic follows an F-distribution.

  • What is \(H_o\)?

  • What are our model conditions?

  • What is a F-distribution?

Null hypothesis

What is our null hypothesis if we want to test if at least one true mean bill length is different across the three species of penguin? What’s the proper notation for it?

Null hypothesis

\(\mu_g = \mu_c = \mu_a\)

Theory based

If \(H_o\) is true and the model conditions are satisfied, an F-statistic follows an F-distribution.

– What is \(H_o\)? ✔️

– What are our model conditions?

– What is a F-distribution?

Model conditions

  • Independence

  • Normality

  • Constant Variance

Independence

Within and between groups

  > Do we have a random sample? 
  > Is there an obvious reason why observatiosn are dependent on each other (ex. space and time)?

Normality

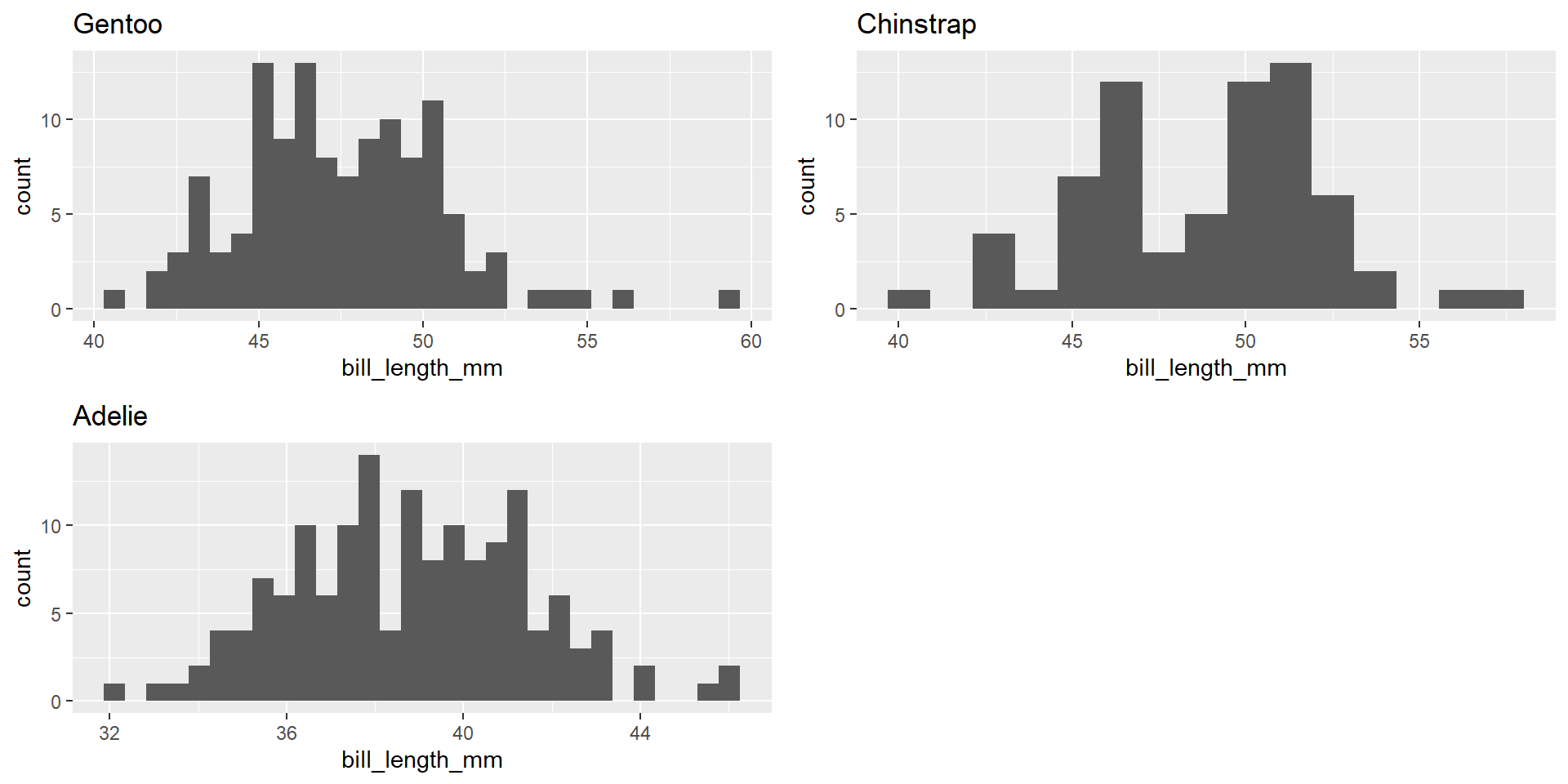
Normality

Outliers?

Sample size

penguins |>
  group_by(species) |>
  summarise(count = n())
# A tibble: 3 × 2
  species   count
  <fct>     <int>
1 Adelie      152
2 Chinstrap    68
3 Gentoo      124

Constant Variance

Are the spreads within each group about the same? The constant variance condition is especially important when the sample sizes differ between groups

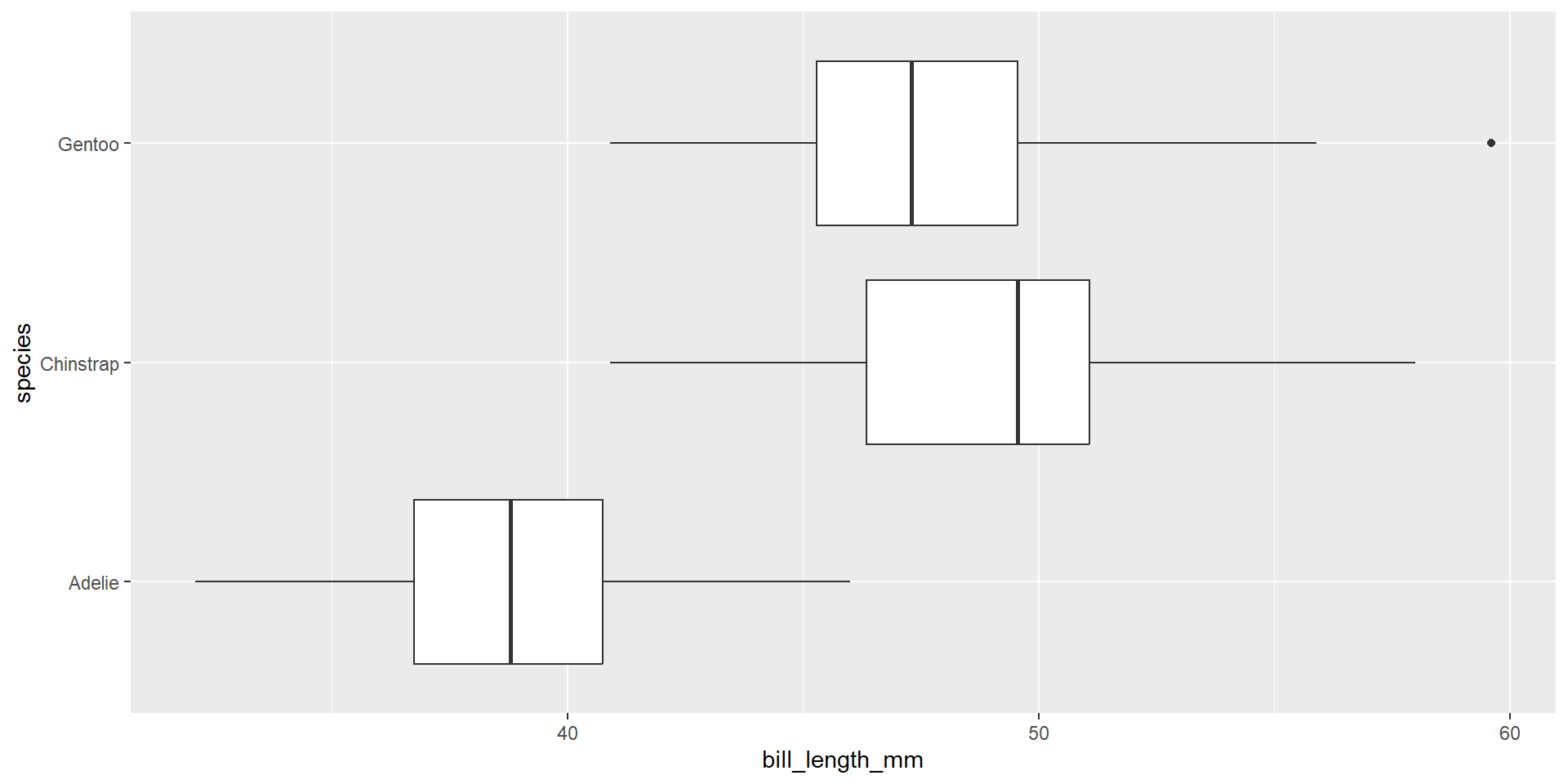
Rule of thumb

To check for equal variances, you can compare the smallest and largest sample standard deviations. A rule of thumb is that the ratio of the largest and smallest sample standard deviations should not exceed 2.

penguins |>
  group_by(species) |>
  summarise(spread = sd(bill_length_mm, na.rm = T))
# A tibble: 3 × 2
  species   spread
  <fct>      <dbl>
1 Adelie      2.66
2 Chinstrap   3.34
3 Gentoo      3.08

Rule of thumb

– Some fields use 3

– Levene test

– Welch one-way test

– Residual vs Fitted plot (we will talk about these types of plots when we get to fitting models)

Theory based

If \(H_o\) is true and the model conditions are satisfied, an F-statistic follows an F-distribution.

– What is \(H_o\)? ✔️

– What are our model conditions? ✔️

– What is a F-distribution?

F-Distribution

– The curve is not symmetrical but skewed to the right.

– There is a different curve for each set of degrees of freedom

– We have two sets of degrees of freedom (df) to specify

  > One for the mean square between groups (k-1) where k is the number of groups (numerator df)
  > One for the mean square (within) error (n-k) where n is the total sample size (denomanator df)

– F-statistics can not be negative

App

Degrees of freedom

Generally, degrees of freedom is equal to the number observations we use to estimate parameters minus the number of parameters we are trying to estimate

I like to think about degrees of freedom as cogs that shape our theoretical distribution based on our observations

Question What are the numerator and denominator degrees of freedom for our penguin study? Hint: our sample size is 342

Degrees of freedom

We have 3 groups (k)

Numerator df = 3 - 1 = 2

We have 342 - 3 = 339

Theory based

If \(H_o\) is true and the model conditions are satisfied, an F-statistic follows an F-distribution.

– What is \(H_o\)? ✔️

– What are our model conditions? ✔️

– What is a F-distribution? ✔️

Alternative hypothesis

\(H_a\) At least one population mean bill length is different

In R

# Compute the analysis of variance
res.aov <- aov(bill_length_mm ~ species, data = penguins)
# Summary of the analysis
summary(res.aov)
             Df Sum Sq Mean Sq F value Pr(>F)    
species       2   7194    3597   410.6 <2e-16 ***
Residuals   339   2970       9                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
2 observations deleted due to missingness

🔗 class website