Bias, Sampling, and Scope of Inference
Second to last!
NC State University
ST 511 - Fall 2024
2024-11-25
Checklist
– Keep up with Slack
– HW 6 has been released (due Tue 26th at 11:59; our last HW!)
– No more quizzes
– Don’t forget about the statistics experience (Due Dec 6th)
– Extra credit for survey exam-1 will be put in at end of semester
– Start filling out your note sheet! Note: formula sheet coming by end of week
– Exam-1 in class corrections are in (Gradescope); I will sync Gradescope to Gradebook sometime this week
– Odds ratio walkthrough posted on our website
Announcements
Class evaluation
Please take time to fill this out: http://go.ncsu.edu/cesurvey
> I take them very seriously, and will read them after the semester
> The department takes them very seriouslyAnnouncements
We are going to have an exam review day on Monday, December 2nd. Please vote via Slack in the announcements channel on how you would like it to be structured! I’ll leave it up until Wednesday or so.
Final Exam
Will be in our assigned room (see Slack for assigned times)
Cumulative with heavy emphasis on unit-2
> The most involved questions will be on unit-2 content
> May see MC questions on unit-1
> Will see questions on content that carry over from unit-1 (p-values; etc)
> May include a coding question or two (similar to exam-1)
> Will start with "pick-a-test" (beginning of hw-3)
Warm Up
– What is a p-value?
– What is a confidence interval?
What do each help us accomplish?
P-value
Definition: Probability of observing our statistic, or something more extreme, given the null hypothesis is true
Compare p-value to \(\alpha\)
> If p-value > alpha, we fail to reject the null hypothesis (decision)
> If p-value is < alpha, we reject the null hypothesis Confidence interval
Definition: Range of plausible values that our population parameter can take on
We create confidence intervals when we want to estimate what’s going on at the population level
> Can look at the signs of the confidence interval
> Can look if the confidence interval contains 0
Questions
Goal for today
Introduce you to topics that you may need in your own research. This includes information on how to talk about your results, types of bias, and sampling schemes.
Setting the stage
In 511, we’ve done both inferential and descriptive statistics!
Descriptive: describe the main features of a dataset without making generalizations about a larger population (creating visualizations, ; summary statistics; interpreting regression coefficients + making predictions)
Inferential: uses data analysis to draw conclusions about a population based on a sample (simulation based hypothesis testing + confidence intervals; z-tests; t-tests; Anova; Chi-Square test)
The Data
The data that we analyze have to come from somewhere! Let’s talk about different sampling schemes
– Random sample
– Stratified sample
– Cluster sample
What’s a random sample?
Random sample
A random sample is taking a sample from a larger population where each observation in that population has an equal chance of being selected!
Random sample
Advantages
– Helps us assume independence
– Helps us generalize to a larger population (more on this later)
Disadvantages
– It’s really hard… could be difficult to actually target a truly large population of interest
Sampling Schemes
– Random sampling ✔️
– Stratified sample
– Cluster sample
Stratified sampling
Sometimes, equal probability across all observations may fail to capture critical sub-populations of interest!
A stratified random sample is formed by first splitting the population in non-overlapping subgroups (called strata) and a random sample is taken within each strata.
Note: the different strata should be diverse; objects within strata should be similar
Advantages and disadvantages
Advantages
– Ensures that the sample contains information about all strata within the population.
– Statistics can be calculated to estimate subgroup parameters in addition to the overall population parameters.
Disadvantages
– Need to know more about the subjects being sampled. Specifically, to which strata they belong.
– More complex calculations required to analyze.
– Random samples are still hard…
Types of sampling
– Random sampling ✔️
– Stratified sampling ✔️
– Cluster sampling
Cluster sampling
A cluster sample is formed by first splitting the population in non-overlapping subgroups (called clusters) and a random sample of clusters is taken and all subjects within selected clusters are sampled.
Note: objects within clusters should be diverse; different clusters should be similar.
Example: we could sample high school students by randomly selecting 10 high schools and talking with all students in those schools.
Advantages and disadvantages
Advantages
– “Easier”: Less resource expense; especially when subjects in a population are geographically spread out.
Disadvantages
– May not represent the population well, depending on clusters sampled
– More complex calculations required to analyze
Convenience sampling
Convenience sampling: a non-random sampling method where participants are selected based on their availability, willingness, or ease of access
– Can be useful in certain situations… but
non-representative (more on this in the following slides)
sampling bias can occur (more on this in the following slides)
Practice
For the following scenario, justify which sampling method you would use and why.
Practice
A large auto parts supplier with distribution centers throughout the United States wants to survey its employees concerning how satisfied/dissatisfied they are with their health insurance coverage.
Employee insurance plans vary greatly from state to state.
The company wants to obtain an estimate of the annual health insurance deductible its employees would find acceptable
Solution
Since insurance plans vary greatly from state to state we would be wise to split the population into groups, with the states serving as the groups.
We know that insurance plans vary greatly between states, which means with respect to the variable of interest, the groups are different. Recall that for cluster sampling the groups are supposed to be similar and the diversity happens within cluster. Since that is not what is happening here we conclude that stratified random sampling is the method of choice for best results.
Types of Bias
Bias
Bias is a term used in statistics that represents some error in data collection, analysis, etc. that may result in inaccurate conclusions.
We are going to focus on the bias in sampling methods.
Types of bias
– Response bias
– Non-response bias
– Sampling bias
Let’s start with the first type. What is response bias?
Response bias
When there is a systematic reason for someone to answer a question incorrectly
What could be an example of this?
Example
Interviewing high school kids about drinking habits
“Do you consume alcohol?”
Bias
– Response bias ✔️
– Non-response bias
– Sampling bias
Non-response bias
When there is a systematic reason that participants are unwilling or unable to respond to a question(s)
What is an example of this?
Non-response bias
– Telemarketers
– Making a questionnaire too long
Bias
– Response bias ✔️
– Non-response bias ✔️
– Sampling bias
Sampling bias
Some members of the intended population have a lower or higher sampling probability
Suppose you were interested in NC State students. What could be an example of sampling bias?
Sampling bias
Any example that has to do with time and space!
Practice
Suppose you are a researcher interested in NC State student’s smoking habits. Give an example of a leading question that may elicit response or non-response bias!
Solution
Given that you can enlist in the military at 17 years old, do you think it’s reasonable for the legal age to buy tobacco products to be 21 years old?
Scope of inference
Scope of Inference
Often written at the end of research/literature. Helps us articulate our findings appropriately.
Are we justified to make inferences at the population level?
Can you establish causal inference between the variables you are interested in?
Population level
If I am interested in the height of NC State students, and I go sample the heights of all the basketball players…. do you think it’s reasonable to take my findings and generalize them to all NC State students?
- Of course not! Why?
Population level
In order to generalize findings to our population using a single sample, our sample has to be representative of said larger population.
How?
Random sampling
We know from prior classes that taking a random sample of observations is a great way to assume independence, but it also helps us make the assumption that our observations are representative!
That is, our sample is an unbiased representation of our population.
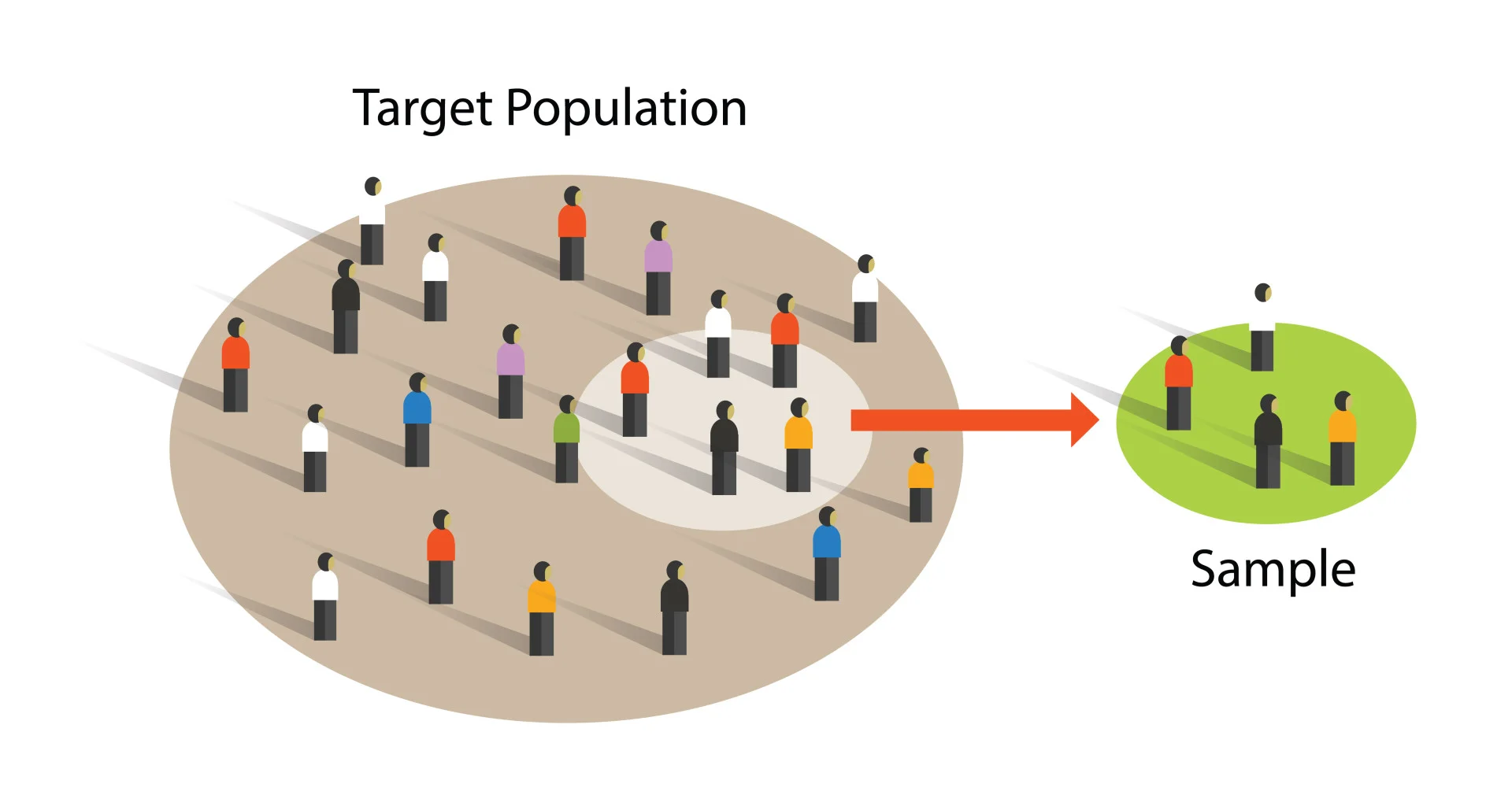
Population level
If you are trying to make generalizations to the larger population, you need to be able to justify that your sample is representative of that larger population. Taking a random sample is the “easiest” way to do this.
If you do not have a random sample, you must be able to reasonably assume and articulate that your sampling scheme has no underlying bias that may make your sample not representative.
Causal inference
Are we justified to say that X causes the changes we see in Y?
Causal inference
We can make this claim if we conduct an experiment that has random assignment of treatments. Why?
Type of study
Experiment
Observational study
Type of study
Experiment - a planned procedure designed to test a hypothesis by manipulating one or more variables under controlled conditions
Observational study - a type of research where researchers observe or collect information
In summary
There is a lot to think about (besides just the methods) during research!
The way you sample data + types of bias that can occur are just two of the many things!