Simulation studies

For difference in proportions

This is code that goes along with the slides from class!

Packages

library(tidymodels)
library(tidyverse)
library(palmerpenguins)

Hypothesis testing

Simulation study for penguin hypothesis test:

x - species

y - sex

\(Ho: \pi_g - \pi_c = 0\)

\(Ha: \pi_g - \pi_c > 0\)

Data

penguin_data <- penguins |>
  filter(species %in% c("Gentoo", "Chinstrap"),
         !is.na(species), 
         !is.na(sex)) |>
  droplevels()

penguin_data |>
  group_by(species, sex) |>
  summarise(size = n())

`summarise()` has grouped output by 'species'. You can override using the
`.groups` argument.

# A tibble: 4 × 3
# Groups:   species [2]
  species   sex     size
  <fct>     <fct>  <int>
1 Chinstrap female    34
2 Chinstrap male      34
3 Gentoo    female    58
4 Gentoo    male      61

penguin_data |>
  select(species, sex)

# A tibble: 187 × 2
   species sex   
   <fct>   <fct> 
 1 Gentoo  female
 2 Gentoo  male  
 3 Gentoo  female
 4 Gentoo  male  
 5 Gentoo  male  
 6 Gentoo  female
 7 Gentoo  female
 8 Gentoo  male  
 9 Gentoo  female
10 Gentoo  male  
# ℹ 177 more rows

The simulation

set.seed(12345)
null_dist <- penguin_data |>
  specify(response = sex, explanatory = species, success = "male") |>
  hypothesize(null = "independence") |>
  generate(reps = 5000, type = "permute") |>
  calculate(stat = "diff in props", order = c("Gentoo", "Chinstrap"))

The plot

null_dist |>
  ggplot(
    aes(x = stat)
  ) + 
  geom_density(fill = "gray")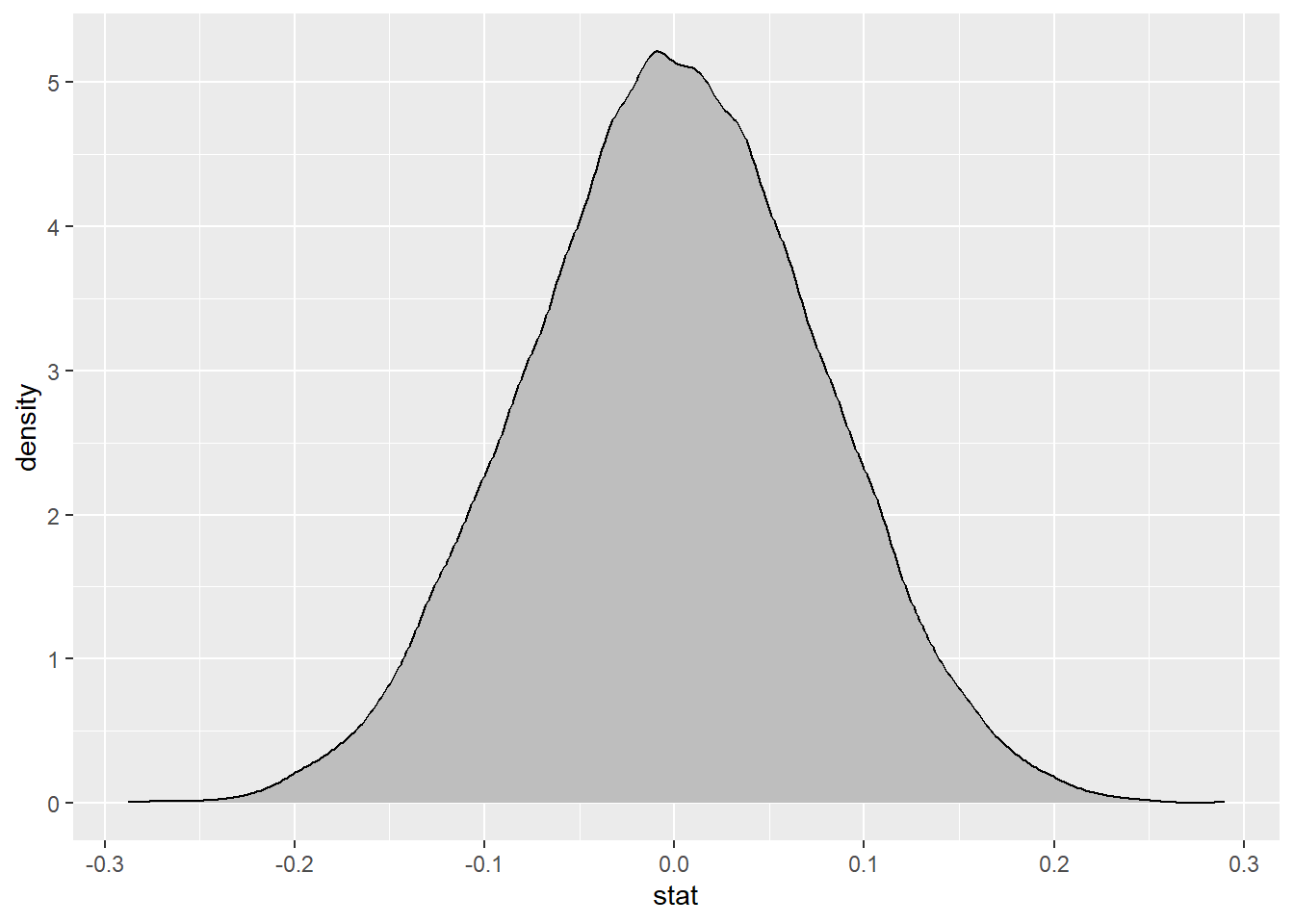

– Where is this centered? Why does this make sense?

This is centered at the null value of 0, because we assume that species and sex are independent.

P-value

null_dist |>
  get_p_value(obs_stat = 0.013, direction = "right")

# A tibble: 1 × 1
  p_value
    <dbl>
1   0.375

visualize(null_dist , bins = 12) +
  shade_p_value(obs_stat = 0.013, direction = "right")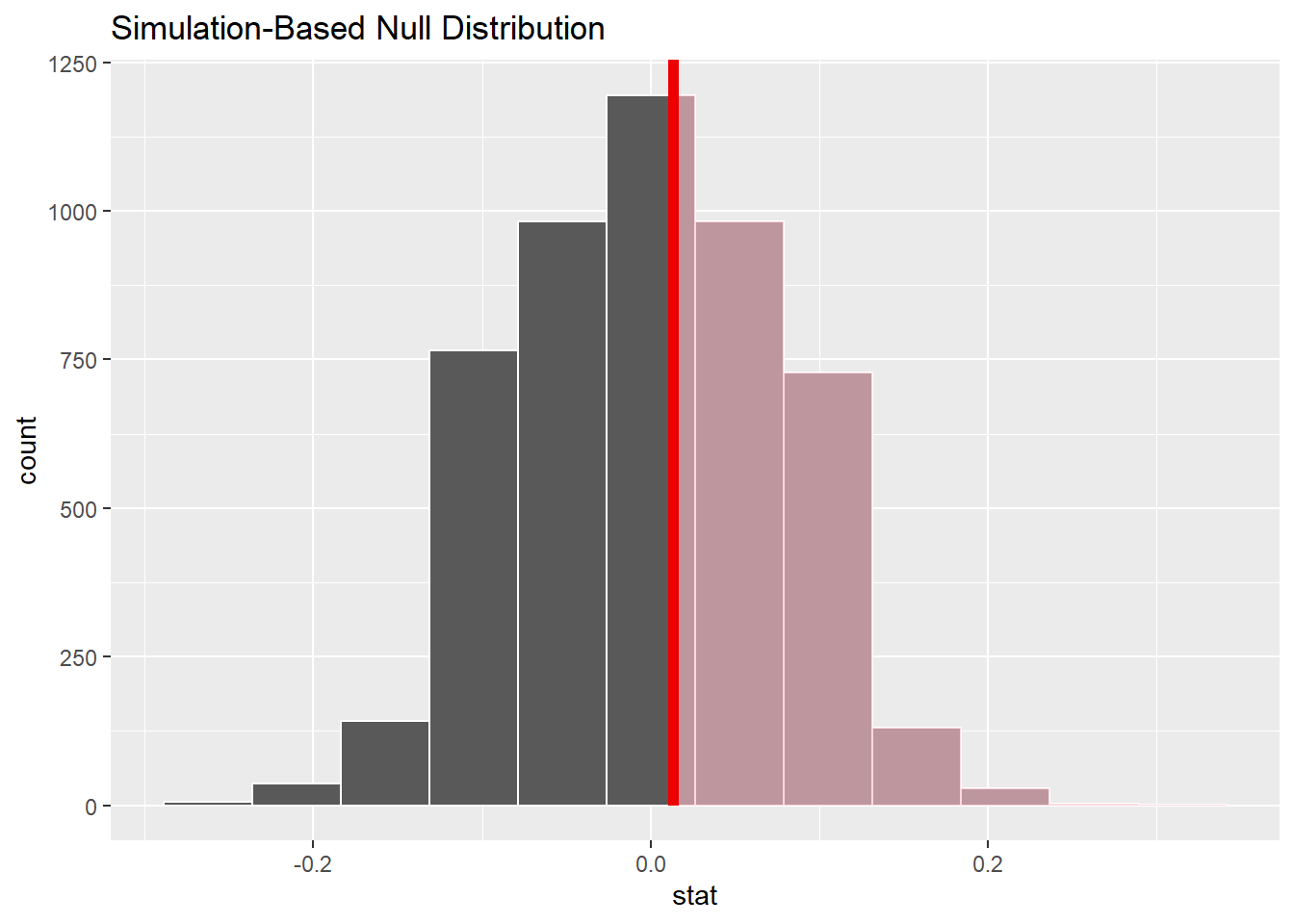

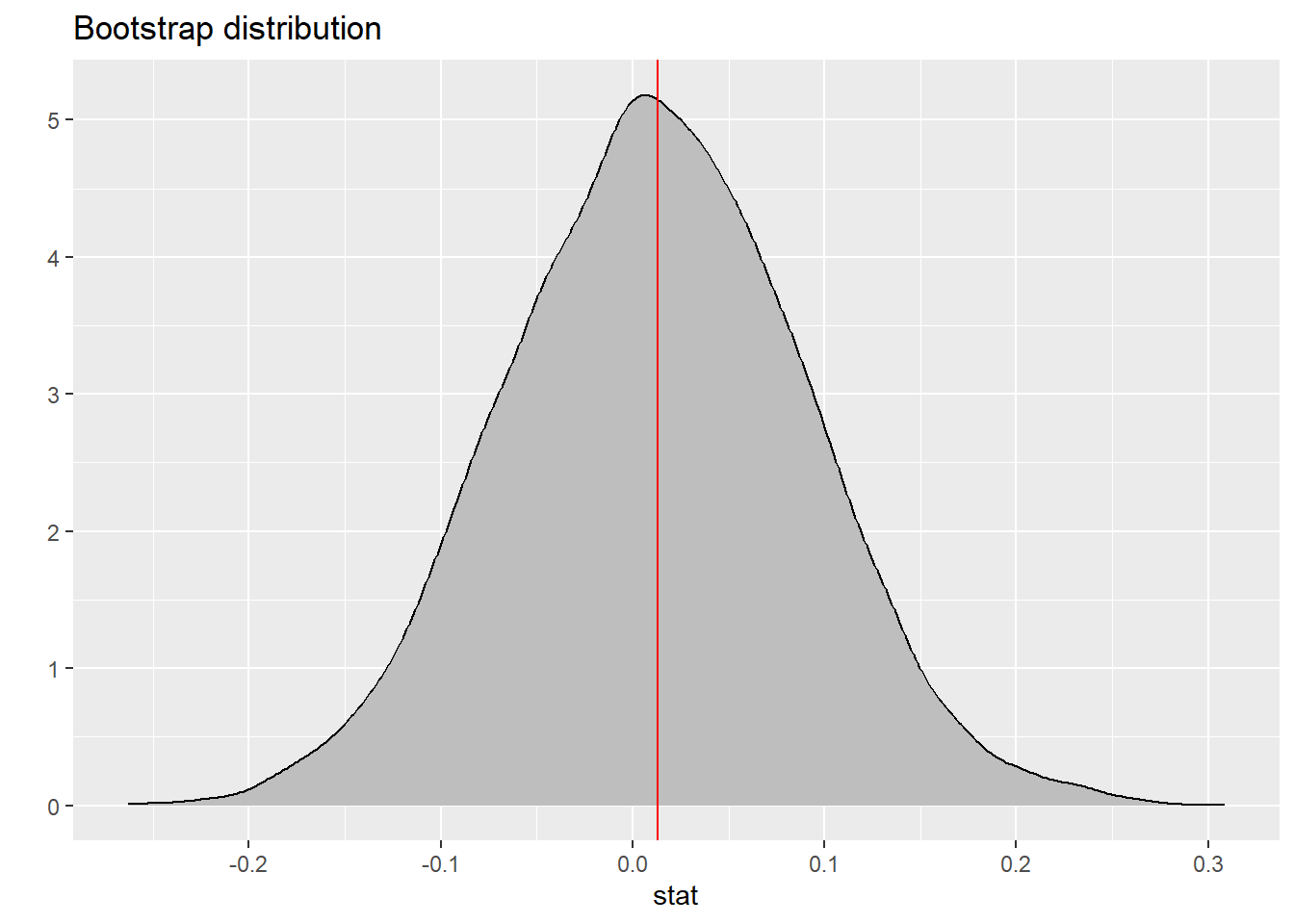
Confidence intervals

set.seed(333)

boot_df <- penguin_data |>
  specify(explanatory = species, response = sex, success = "male") |>
  generate(reps = 10000, type = "bootstrap") |>
  calculate(stat = "diff in props", order = c("Gentoo", "Chinstrap"))

The Graph

boot_df |>
  ggplot(
    aes(x = stat)
  ) + 
  geom_density(fill = "gray") +
  labs(title = "Bootstrap distribution",
       y = "") + 
  geom_vline(xintercept = 0.013, color = "red")

The Calculation

boot_df |>
  summarize(lower = quantile(stat, 0.025),
            upper = quantile(stat, 0.975))

# A tibble: 1 × 2
   lower upper
   <dbl> <dbl>
1 -0.140 0.165