HW 3: Pick-a-test + Anova Solutions

& exam corrections

Homework

Important

This homework is due Sunday, Nov 3 at 11:59pm.

Packages

library(tidyverse)
library(openintro)
library(tidymodels)
library(multcomp)

Tips

Remember that continuing to develop a sound workflow for reproducible data analysis is important as you complete this homework and other assignments in this course. There will be reminders in this assignment for you to Render your document. The last thing you want to do is work an entire assignment before realizing you have an error somewhere that makes it so you can’t compile your document. Render after each completed question.

Note

Note: Do not let R output answer the question for you unless the question specifically tells you to do so.

Note

Note: You can not earn more than 100% on this assignment. Exam corrections can not give you more than a 100% on the exam afte corrections.

Exercises

Exercise 1: Pick-a-test

I am going to present you with 4 different scenarios. For EACH scenario, you are going to:

– Identify the scenario, and justify why. Scenarios include

  > single mean 
  > difference in mean 
  > single proportion
  > difference in proportion 
  > ANOVA

– Write out the null hypothesis for the identified scenario in properer notation

Hint: You may need to explore the data set to identify the scenario. You may also pull up the help file by typing ?data.set.name in your console.

Scenario 1: This data set is called PlantGrowth. This data set contains results from an experiment to compare yields (as measured by dried weight of plants) explained by if the plant was given a control, or different treatment conditions.

Answer This scenario is Anova because we have a quantitative response and a categorical explanatory variable with > 2 levels. The null hypothesis would be \(Ho: \mu_c = \mu_1 = \mu_2\)

Scenario 2: This data set is called mtcars. The data was extracted from the 1974 Motor Trend US magazine, and comprises fuel consumption and 10 aspects of automobile design and performance for 32 automobiles (1973–74 models). You are interested in investigating if the Engine shape of the car has an impact of the car’s miles per gallon.

Answer This scenario is difference in means because we have a quantitative response with a categorical variable that has = 2 levels. The null hypothesis would be \(Ho: \mu_v = \mu_s\)

Scenario 3: This data set is called HairEyeColor. This data set contains hair and eye color and sex in 592 statistics students. Suppose researchers were just interested in Female students. Researchers theorized that the a female’s hair color impacted the color of their eyes. Specifically, they wanted to investigate if females with darker hair (black or brown) had darker color of eyes (brown or hazel) compared to females with lighter hair (red or blond).

Answer This scenario is difference in proportions because we have a categorical response variable and categorical explanatory variable both with 2 levels. The null hypothesis would be \(Ho: \pi_d = \pi_l\)

Scenario 4: This data set is called iris. This famous (Fisher’s or Anderson’s) iris data set gives the measurements in centimeters of the variables sepal length and width and petal length and width, respectively, for 50 flowers from each of 3 species of iris. The species are Iris setosa, versicolor, and virginica. We are interested in investigating if the mean sepal length is larger than 6mm.

Answer This scenario would be single mean. We have a single quantitative variable that we are interested in. The null hypothesis would be \(Ho: \mu = 6\)

Exercise 2 - Tooth Growth

We are going to work with a similar data set as you saw on exam-1, but in a different way. This data set is called ToothGrowth. The response is the length of odontoblasts (cells responsible for tooth growth) in 60 guinea pigs. Each animal received one of three dose levels of vitamin C (0.5, 1, and 2 mg/day) by one of two delivery methods, orange juice or ascorbic acid (a form of vitamin C and coded as VC).

First, we are going to combine the supp and dose column together so we create one variable that has six different combinations of supplement by dose. Use the new_tooth data set to verify that we have six levels of our new treatment variable with n = 10 for each treatment. Hint: make a tibble of count of the new treatment variable.

new_tooth <- ToothGrowth |>
  unite(col = "treatment", supp, dose, sep = "_") |>
  mutate(treatment = factor(treatment))

new_tooth |>
  group_by(treatment) |>
  summarise(count = n())

# A tibble: 6 × 2
  treatment count
  <fct>     <int>
1 OJ_0.5       10
2 OJ_1         10
3 OJ_2         10
4 VC_0.5       10
5 VC_1         10
6 VC_2         10

Create side-by-side boxplots of these data. Comment on the overall pattern. That is, what is the relationship between tooth growth and the treatment variable?

new_tooth |>
  ggplot(
    aes(x = treatment, y = len)
  ) + 
  geom_boxplot() + 
  labs(title = "Boxplots of tooth growth in 60 guinea pigs by treatment",
       x = "Treatment combo",
       y = "tooth growth length")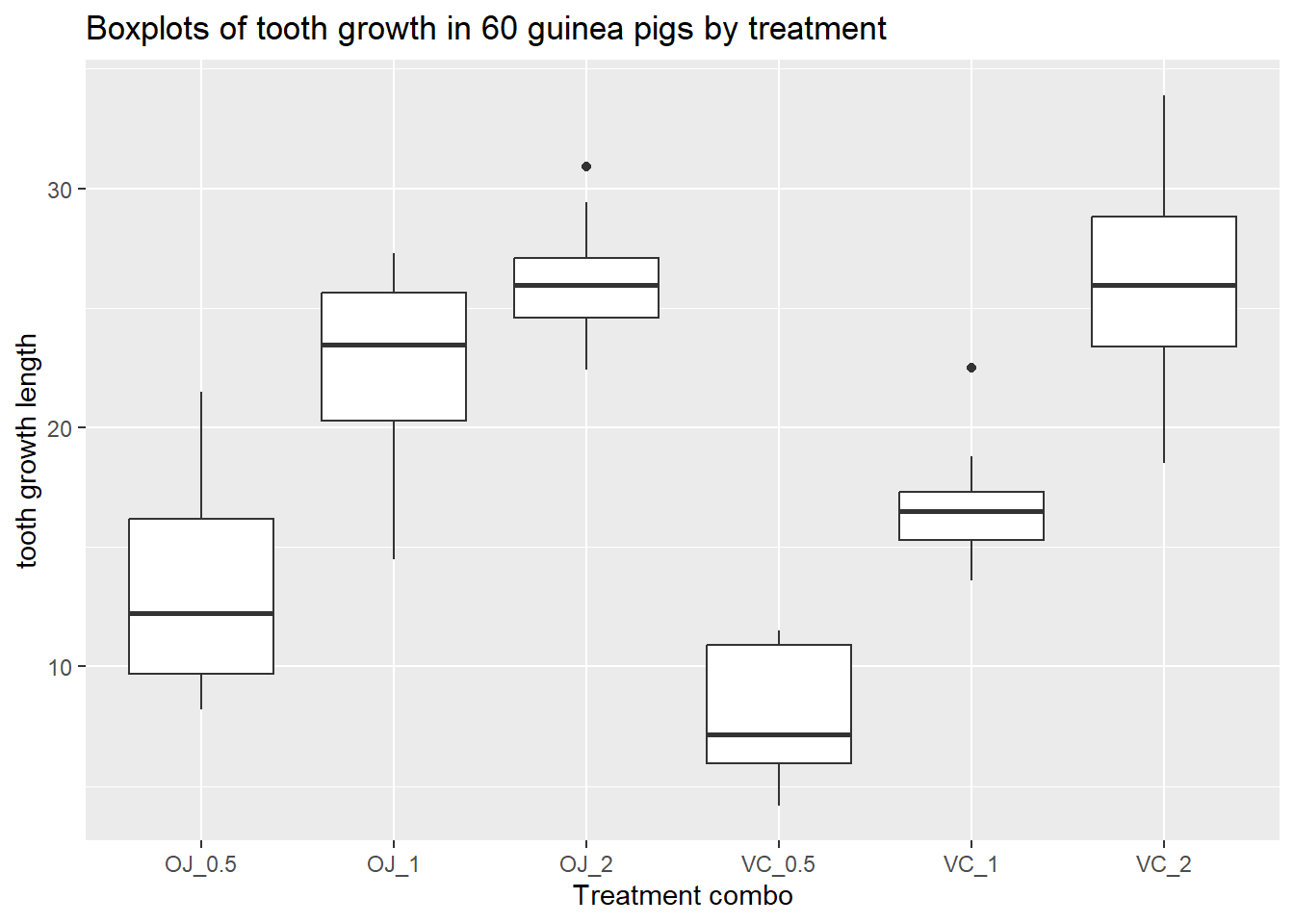

Answer It appears that, regardless of OJ or VC, tooth growth increases as the dosage increases. AWV: Something reasonable.

Before checking assumptions, we need to set up our null and alternative hypotheses. Write out, in proper notation, the null and alternative hypothesis for this question. Note: Please use informative subscripts or define them.

Answer

\(Ho: \mu_\text{oj05} = \mu_\text{oj1} = \mu_\text{oj2} = \mu_\text{vc05} = \mu_\text{vc1} = \mu_\text{vc2}\)

Ha: At least one population mean tooth length is not equal.

We are now going to check our validity condition: Independence, constant variance, and normality. When checking for independence, we are are going to assume that the guinea pigs were kept in separate cages. If the experiment had the animals in separate cages, there is no clear dependency in the design of the study and can assume that there is no problem with this assumption.

Use the box plots to check the assumption of normality from part b. Then, use the given table to check the constant variance assumption.

new_tooth |>
  group_by(treatment) |>
  summarise(sd = sd(len))

# A tibble: 6 × 2
  treatment    sd
  <fct>     <dbl>
1 OJ_0.5     4.46
2 OJ_1       3.91
3 OJ_2       2.66
4 VC_0.5     2.75
5 VC_1       2.52
6 VC_2       4.80

Answer

Normality: It appears that there could be some evidence that the normality assumption is violated, because we see one outlier in both the OJ2 and VC1 group, and our sample size is only 10. OR There is not enough evidence to violate the normality assumption. Most of the boxplots look symmetric, and there are only two groups that have a single outlier (either can be correct as long as correct justification).

Constant vairance: It appears that the box plots do have different spread (IQR). The ratio between the largest and smallest sd for these data are 4.80/2.66 = 1.80. With the rule of thumb being < 2, we do not have enough evidence to reject the constant variance assumption.

Regardless of your assumptions, we are going to carry out an ANOVA. The code for this can be seen below:

res.aov <- aov(len ~ treatment, data = new_tooth)

summary(res.aov)

            Df Sum Sq Mean Sq F value Pr(>F)    
treatment    5 2740.1   548.0   41.56 <2e-16 ***
Residuals   54  712.1    13.2                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Using this information, report the f-statistic, p-value, and the distribution that the p-value was calculated from. Hint: be specific!

Answer

The F-statistic is 41.56. The p-value was calculated to be < 0.001 from an F-distribution with 5 and 54 degrees of freedom.

Write an appropriate decision AND conclusion in the context of the problem.

Answer

We reject the null hypothesis, and have strong evidence to conclude that at least one population mean tooth growth differs across our treatment combos.

Exercise 3: Tukey

Regardless of your conclusion, we are going to conduct a Tukey’s HSD test to investigate which means (if any), are significantly different from each other.

In detail, please explain why we are using Tukey’s HSD to investigate this question, instead of conducting many individual t-tests?

Answer

We are using Tukey’s to account for an inflated type 1 error that would come up if we conducted a bunch of individual t-tests.

How many pairwise comparisons (aka hypothesis tests for difference in means) do we have in this study? Hint: Use the choose() function to help figure this out. The syntax for the choose() is choose(total groups, number of groups being compared for one hypothesis test).

Answer

choose(6, 2)

[1] 15

Below are the results for Tukey HSD, with assocciated 95% confidence intervals.

pig_tukey <- TukeyHSD(res.aov)

pig_tukey

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = len ~ treatment, data = new_tooth)

$treatment
                diff        lwr         upr     p adj
OJ_1-OJ_0.5     9.47   4.671876  14.2681238 0.0000046
OJ_2-OJ_0.5    12.83   8.031876  17.6281238 0.0000000
VC_0.5-OJ_0.5  -5.25 -10.048124  -0.4518762 0.0242521
VC_1-OJ_0.5     3.54  -1.258124   8.3381238 0.2640208
VC_2-OJ_0.5    12.91   8.111876  17.7081238 0.0000000
OJ_2-OJ_1       3.36  -1.438124   8.1581238 0.3187361
VC_0.5-OJ_1   -14.72 -19.518124  -9.9218762 0.0000000
VC_1-OJ_1      -5.93 -10.728124  -1.1318762 0.0073930
VC_2-OJ_1       3.44  -1.358124   8.2381238 0.2936430
VC_0.5-OJ_2   -18.08 -22.878124 -13.2818762 0.0000000
VC_1-OJ_2      -9.29 -14.088124  -4.4918762 0.0000069
VC_2-OJ_2       0.08  -4.718124   4.8781238 1.0000000
VC_1-VC_0.5     8.79   3.991876  13.5881238 0.0000210
VC_2-VC_0.5    18.16  13.361876  22.9581238 0.0000000
VC_2-VC_1       9.37   4.571876  14.1681238 0.0000058

Are VC_0.5 and OJ_0.5 detectably different? What about OJ_1 and OJ_0.5? Justify your answer.

Answer

Yes, VC_0.5 and OJ_0.5 are detectably different. We have a small p-value (< \(\alpha\) = 0.05) AND our confidence interval does not estimate 0 to be a plasuible value. Note: students can use one or the other or both as justificaiton.

(Extension question) It is hard to interpret all of Tukey’s output at once. Thus, a common strategy is to use a “compact letter display.” This really helps you present these results to a general audience. This can be done using the following code:

model <- lm(len ~ treatment,data=new_tooth)

Tm2 <- glht(model, linfct = mcp(treatment = "Tukey"))

cld(Tm2)

OJ_0.5   OJ_1   OJ_2 VC_0.5   VC_1   VC_2 
   "a"    "b"    "b"    "c"    "a"    "b"

Groups with the same letter are not detectably different (are in the same set) and groups that are detectably different get different letters (different sets). Groups can have more than one letter to reflect “overlap” between the sets of groups and sometimes a set of groups contains only a single treatment level.

Note that if the groups have the same letter, this does not mean they are the same, just that there is no evidence of a difference for that pair

Questions

Are OJ_05 and VC_1 detectably different? Justify your answer.

Answer No, OJ_05 and VC_1 are not detectably different from each other based on the compact letter display. Both share the same letter.

Is any mean tooth length NOT detectably different from VC_05? Justify your answer.

Answer Every treatment group is detectably different than VC_05. This is the only treatment with the letter c.

Exercise 4 - Anova Table

Suppose you are a researcher interested in looking at carbon dioxide uptake in plants. You design a study that has 12 different types of plants, with 10 observations for each of the 12 different types. You are studying if the type of plant impacts the uptake in CO2.

A partial Anova table can be seen below.

	Df	Sum Sq	Mean Sq	F value	Pr (> F)
plant	a1	6147	a3	a5	a6
Residuals	a2	1988	a4

Use the context of the problem + the relationship between the columns to fill out the remaining table (ex. replace a1 with the actual value). Note a6 can be an estimate.

Answer

	Df	Sum Sq	Mean Sq	F value	Pr (> F)
plant	11	6147	558.82	30.35	< 0.001
Residuals	108	1988	18.41

Exam Corrections (Optional)

This part of the homework assignment is optional. You may earn up to 6 points of your in-class exam grade back by completing this portion of the homework. Note: The primary purpose of exam corrections is not to boost grade scores, but instead give everyone a second opportunity to revisit key statistics topics that I hope you leave class with a full understanding of.

There is no partial credit to these problems. You either earn the full amount of points or zero.

You are allowed to work together, use notes, etc.

Question 1 (1 points)

For this question, we are going to be investigating cars. The data give the speed of cars and the distances taken to stop. Note that the data were recorded in the 1920s. Speed is measured in mph and distance is measured in feet. We are interested in speed’s impact on stopping distance. We are going to see if cars moving slowly (driving between 1 and 19 mph) had shorter stopping distances than those driving between (20 and 25 mph).

Write the correct null and alternative hypothesis below using proper notation. Note, you do not need to write this out in words… just use proper notation.

Answer \(Ho: \mu_s = \mu_f\)

\(Ha: \mu_s < \mu_f\)

Question 2 (1 point)

# A tibble: 2 × 3
  speed_cat distance sample_size
  <chr>        <dbl>       <int>
1 fast          69.3          12
2 slow          34.7          38

Use the following summary table to write out your summary statistic in proper notation.

Answer

\(\bar{x_s} - \bar{x_s} = 34.7 - 69.3\) = -34.6 (note order of subtraction just needs to match their hypothesis above)

Question 3 (2 points)

Use your sample statistic from question 2 to answer this problem. If you could not answer question 2, use the sample statistic of -10. Suppose the researchers conducted a hypothesis test to test your hypotheses set up in question 1, and calculated a p-value of .158. Fill in the banks to appropriately describe how this p-value was calculated in the context of the problem. There are guiding questions below to help you think critically about this interpretation:

blank 1: What even is a p-value? What does the p stand for?

blank 2: How is the calculation of the p-value started. What do we find on our simulated sampling distribution?

blank 3: what area under the curve are we calculating?

blank 4: What assumption do we make (in context) when conducting a hypothesis test?

0.158 represents the ______ of observing _______, or something even ______, given _______

Answer 0.158 represents the probability of observing -34.6, or something even smaller, given the true mean stopping speed for slow moving cars is equal to the true mean stopping speed for fast moving cars.

Question 4 (1 point)

Suppose instead of doing a simulation test, the researchers conducted a theory based test. What named distribution would the test statistic for this specific study follow? Be specific.

Answer A t-distribution with 11 degrees of freedom. We will accept a t-distribution with 48 degress of freeom.

Question 5 (1 point)

Suppose new researchers conduct an entirely separate cars study. They then calculate a confidence interval of (24.34, 56.98). Based on this information, what is the new researchers sample statistic? Then, write a short 1-2 sentences on how you know this.

Answer I know, from this confidence interval, that the sample statistic for the new researchers is equal to 40.66. This is because 40.66 is the center of their confidence interval, and our sample statistic is always in the center of our confidence interval.

Submission

Go to http://www.gradescope.com and click Log in in the top right corner.
Log in with your school credentials.
Click on your STA 511 course.
Click on the assignment, and you’ll be prompted to submit it.
Mark all the pages associated with exercise. All the pages of your homework should be associated with at least one question (i.e., should be “checked”). If you do not do this, you will be subject to lose points on the assignment.
Do not select any pages of your PDF submission to be associated with the “Workflow & formatting” question.

Note

The “Workflow & formatting” grade is to assess the reproducible workflow. This includes:

linking all pages appropriately on Gradescope
putting your name in the YAML at the top of the document
Pipes %>%, |> and ggplot layers + should be followed by a new line
You should be consistent with stylistic choices, e.g. %>% vs |>

Grading for HW-3

Exercise 1: 20 points
Exercise 2: 20 points
Exercise 3: 14 points
Exercise 4: 12 points
Workflow + formatting: 5 points
Total: 71 points