HW 5 - Modelling: Solutions
Packages
We’ll use the tidyverse package for much of the data wrangling and visualization, though you’re welcomed to also load other packages as needed.
Data
For this homework, we are interested in the impact of smoking during pregnancy.
We will use the dataset births14, included in the openintro loaded at the beginning of the assignment. This is a random sample of 1,000 mothers from a data set released in 2014 by the state of North Carolina about the relation between habits and practices of expectant mothers and the birth of their children. Please, look at help(births14) for the variables contained in the dataset.
We are going to create a version of the births14 data set that drops NA values for the variable name habit. We are saving this as a new data set called births14_habitgiven. This will be the data set we use moving forward.
births14_habitgiven <- births14 |>
drop_na(habit) #drop_na drops na values for just a single colExercise 1
Call:
lm(formula = weight ~ mage, data = births14_habitgiven)
Residuals:
Min 1Q Median 3Q Max
-6.4598 -0.6449 0.1205 0.8250 3.1803
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.775362 0.207947 32.582 <2e-16 ***
mage 0.014979 0.007173 2.088 0.037 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.291 on 979 degrees of freedom
Multiple R-squared: 0.004435, Adjusted R-squared: 0.003418
F-statistic: 4.361 on 1 and 979 DF, p-value: 0.03703R fits this the “line of best fit” by fitting the line that minimizes the sums of squares residuals.
On average, when the mother’s age is 0, the estimated weight of the baby is estimated to be 6.78 pounds. This is clear extrapolation, as there is no data around a mother’s age of 0.
Note: Can also say “mean weight” instead of on average to reflect the response variable is a mean.
- For a one year increase in mother’s age, we estimate on average, a 0.015 pound increase in the baby’s weight.
Note: Can also say “mean weight” instead of on average to reflect the response variable is a mean.
Exercise 2 - LEGO
lego_sample <- read_csv("data/lego_sample.csv")The correlation coefficient between the number of pieces of a Lego set and the price on Amazon is 0.6682458, indicating a rather moderate/strong positive linear relationship between the two variables.
s_price <- lego_sample |>
summarize(s_price = sd(amazon_price))
s_piece <- lego_sample |>
summarize(s_piece = sd(pieces))
s_price# A tibble: 1 × 1
s_price
<dbl>
1 33.3s_piece# A tibble: 1 × 1
s_piece
<dbl>
1 214.
Call:
lm(formula = amazon_price ~ pieces, data = lego_sample)
Residuals:
Min 1Q Median 3Q Max
-36.972 -13.671 -5.218 3.767 99.070
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 18.95675 3.92258 4.833 7.24e-06 ***
pieces 0.10403 0.01355 7.675 5.74e-11 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 24.94 on 73 degrees of freedom
Multiple R-squared: 0.4466, Adjusted R-squared: 0.439
F-statistic: 58.9 on 1 and 73 DF, p-value: 5.744e-11The model estimates the following relation:
\[ \widehat{price} = 18.96 + 0.1*pieces \]
Note: They do not need to use LaTex to write this out. They should have something to indicate that this is an estimated response (hat).
\(R^2\) = 0.447
r^2 r
1 0.4465525The coefficient of determination for the previous model is equal to the square of the correlation coefficient and they are both approximately \(0.447\). This means that linear model with only number of pieces as predictor explains around \(45\%\) of the variability in the data (our response, price).
47.7% of the variability in our response price is explained by our linear model including number of pieces
To verify the relation, note that \(\widehat{\beta_{piceces}}=0.104\) from the previous exercise and
r*s_price/s_piece r
1 0.1040297gives the same value, thus the relation is verified.
Exercise 3 - LEGO
lego_sample |>
ggplot(aes(x=pieces, y=amazon_price, col=theme)) +
geom_point() +
geom_smooth(method = "lm", se = F) +
labs(x = "Number of Pieces", y = "Amazon Price", col = "Theme",
title = "Amazon Price and Number of Pieces of Lego Sets by Theme")`geom_smooth()` using formula = 'y ~ x'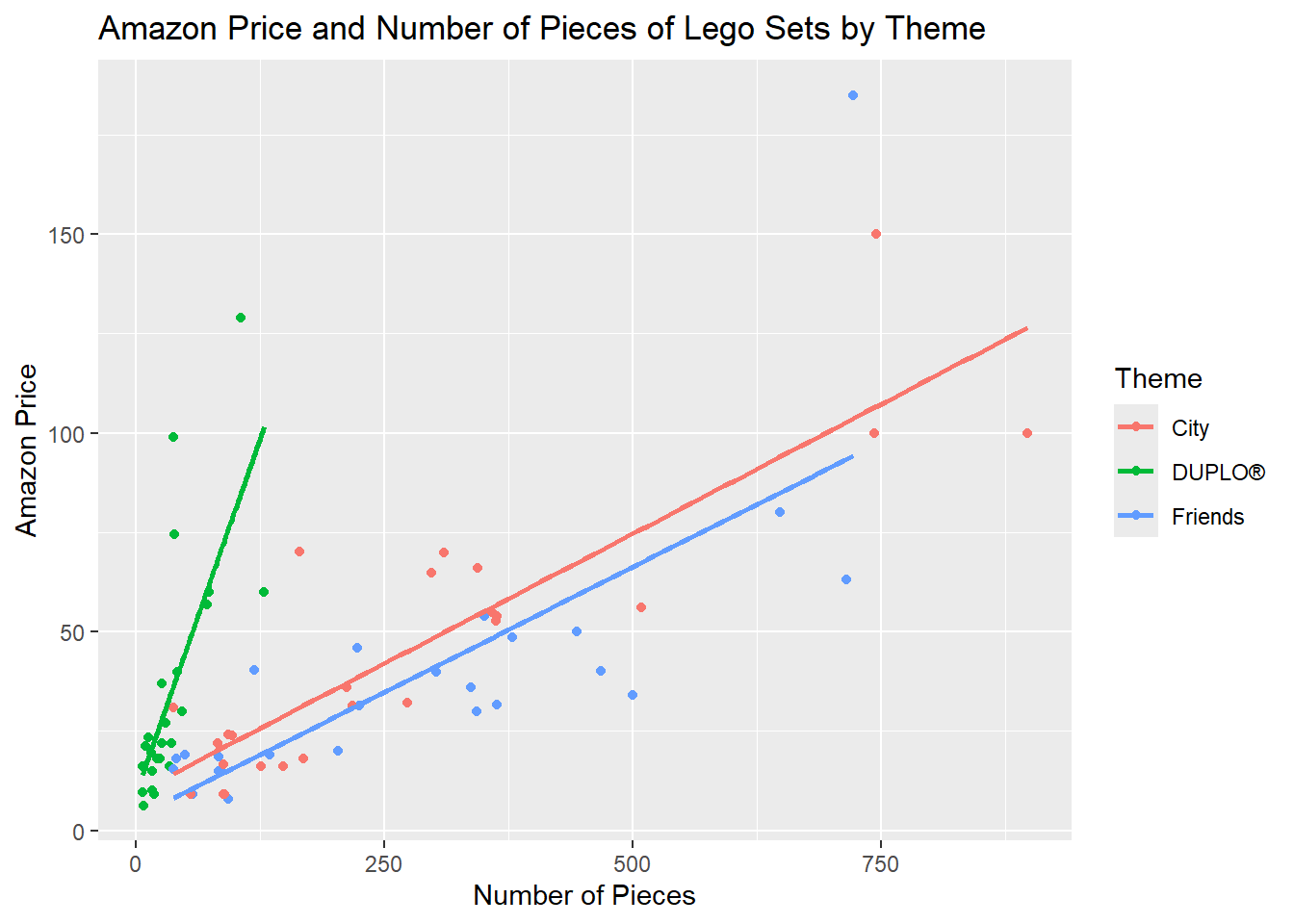
Note: They do not have to take the se bars off, but I anticipate most will, as this is what we have done in class.
From the plot it seems that across all sets, the Price increases as the number of pieces does. However, it seems that how much the price increases for the same increase in the number of pieces varies across the three themes. In particular, the steepest increase seems to happen for Lego Duplo, then for Lego City and lastly for Lego Friends.
Call:
lm(formula = amazon_price ~ pieces + theme, data = lego_sample)
Residuals:
Min 1Q Median 3Q Max
-34.068 -12.736 -5.623 6.056 87.219
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.52364 6.14050 1.388 0.16945
pieces 0.13380 0.01482 9.025 2.11e-13 ***
themeDUPLO® 21.10939 7.41084 2.848 0.00574 **
themeFriends -7.35361 6.50107 -1.131 0.26180
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 22.98 on 71 degrees of freedom
Multiple R-squared: 0.543, Adjusted R-squared: 0.5237
F-statistic: 28.12 on 3 and 71 DF, p-value: 4.281e-12For a 1 piece increase in the number of pieces, we estimate on average a $0.134 increase in amazon price, after holding theme constant.
Note: Can also say “mean price” instead of on average to reflect the response variable is a mean.
- \(\hat{price} = 8.52 + .13*pieces - 7.35\)
\(\hat{price} = 1.17 + .13*pieces\)
predict(model3, data.frame(pieces = 50, theme = "Friends")) 1
7.859872